DepGraph: Towards Any Structural Pruning

概要

结构化剪枝通过从神经网络中删除结构化分组的参数来实现模型加速。然而，参数分组模式在不同的模型中存在很大差异，这使得特定于体系结构的修剪器依赖于手工设计的分组方案，无法推广到新的体系结构中。

本工作在结构化剪枝的自动化上做了改进，提出了一种非深度图算法DepGraph，实现了架构通用的结构化剪枝，适用于CNNs,，Transformers, RNNs, GNNs等网络。DepGraph能够显式地建模层之间的依赖关系，并对耦合参数进行综合剪枝。自动地分析复杂的结构耦合，从而正确地移除参数实现网络加速。基于DepGraph算法，作者开发了PyTorch结构化剪枝框架 Torch-Pruning。不同于依赖Masking实现的“模拟剪枝”，该框架能够实际地移除参数和通道，降低模型推理成本。在DepGraph的帮助下，研究者和工程师无需再与复杂的网络结构斗智斗勇，可以轻松完成复杂模型的一键剪枝。

本文在几个架构和任务包括ResNe (X)t，DenseNet，MobileNet，VIT，GAT，DGCNN，LSTM上进行广泛评估。并证明提出的方法始终产生令人满意的性能。

前置知识

模型部署优化：通过减小模型大小，提高推理速度等，使得模型能够成功部署在各个硬件之中去并且实时有效的运作

模型剪枝

深度学习网络模型从卷积层到全连接层存在着大量冗余的参数，大量神经元激活值趋近于0，将这些神经元去除后可以表现出同样的模型表达能力，这种情况被称为过参数化，而对应的技术则被称为模型剪枝。

Dropout和DropConnect代表着非常经典的模型剪枝技术。

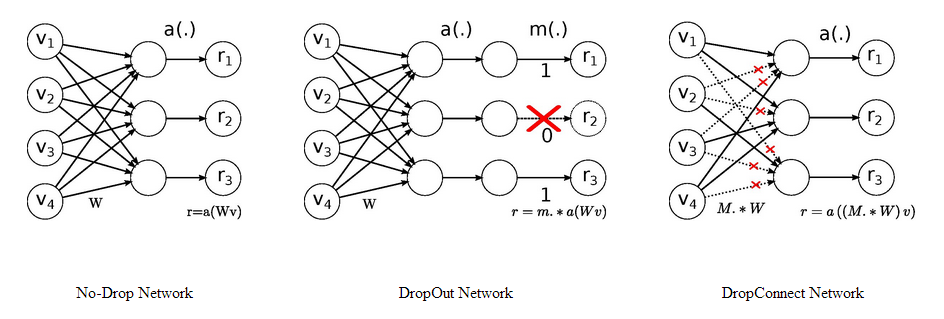
Dropout中随机的将一些神经元的输出置零，这就是神经元剪枝。DropConnect则随机的将一些神经元之间的连接置零，使得权重连接矩阵变得稀疏，这便是权重连接剪枝。它们就是最细粒度的剪枝技术，只是这个操作仅仅发生在训练中，对最终的模型不产生影响，因此没有被称为模型剪枝技术。

当然，模型剪枝不仅仅只有对神经元的剪枝和对权重连接的剪枝，根据粒度的不同，至少可以粗分为4个粒度。

• 细粒度剪枝(fine-grained)：即对连接或者神经元进行剪枝，它是粒度最小的剪枝。
• 向量剪枝(vector-level)：它相对于细粒度剪枝粒度更大，属于对卷积核内部(intra-kernel)的剪枝。
• 核剪枝(kernel-level)：即去除某个卷积核，它将丢弃对输入通道中对应计算通道的响应。
• 滤波器剪枝(Filter-level)：对整个卷积核组进行剪枝，会造成推理过程中输出特征通道数的改变。

细粒度剪枝(fine-grained)，向量剪枝(vector-level)，核剪枝(kernel-level)方法在参数量与模型性能之间取得了一定的平衡，但是网络的拓扑结构本身发生了变化，需要专门的算法设计来支持这种稀疏的运算，被称之为非结构化剪枝。

而滤波器剪枝(Filter-level)只改变了网络中的滤波器组和特征通道数目，所获得的模型不需要专门的算法设计就能够运行，被称为结构化剪枝。除此之外还有对整个网络层的剪枝，它可以被看作是滤波器剪枝(Filter-level)的变种，即所有的滤波器都丢弃。

Google在《To prune, or not to prune: exploring the efficacy of pruning for model compression》[1]中探讨了具有同等参数量的稀疏大模型和稠密小模型的性能对比，在图像和语音任务上表明稀疏大模型普遍有更好的性能。

步骤

• 首先训练一个大模型至最佳性能。
• 对模型的权重进行分析，去除那些对模型输出影响最小的权重。
• 对经过剪枝的模型重新进行微调，以恢复因剪枝造成的性能下降。

模型量化

我们知道为了保证较高的精度，大部分的科学运算都是采用浮点型进行计算，常见的是32位浮点型和64位浮点型，即float32和double64。

对于深度学习模型来说，乘加计算量是非常大的，往往需要GPU等专用的计算平台才能实现实时运算，这对于端上产品来说是不可接受的，而模型量化是一个有效降低计算量的方法。

量化，即将网络的权值，激活值等从高精度转化成低精度的操作过程，例如将32位浮点数转化成8位整型数int8，同时我们期望转换后的模型准确率与转化前相近。

模型量化可以带来几方面的优势，如下。

(1) 更小的模型尺寸。以8bit量化为例，与32bit浮点数相比，我们可以将模型的体积降低为原来的四分之一，这对于模型的存储和更新来说都更有优势。

(2) 更低的功耗。移动8bit数据与移动32bit浮点型数据相比，前者比后者高4倍的效率，而在一定程度上内存的使用量与功耗是成正比的。

(3) 更快的计算速度。相对于浮点数，大多数处理器都支持8bit数据的更快处理，如果是二值量化，则更有优势。

知识蒸馏

一般地，大模型往往是单个复杂网络或者是若干网络的集合，拥有良好的性能和泛化能力，而小模型因为网络规模较小，表达能力有限。利用大模型学习到的知识去指导小模型训练，使得小模型具有与大模型相当的性能，但是参数数量大幅降低，从而可以实现模型压缩与加速，就是知识蒸馏与迁移学习在模型优化中的应用。Hinton等人最早在文章“Distilling the knowledge in a neural network”中提出了知识蒸馏这个概念，其核心思想是一旦复杂网络模型训练完成，便可以用另一种训练方法从复杂模型中提取出来更小的模型，因此知识蒸馏框架通常包含了一个大模型(被称为teacher模型)，和一个小模型(被称为student模型)。

具体的方法是在训练小模型时，在损失函数中添加额外的损失函数，损失函数的添加方式有以下几种：

1.输出层的差异损失：这种方法是对比学生网络和教师网络在输出层上的概率分布之间的差异；

2.隐藏层的相似度损失（余弦相似度损失）：这种方法是对比学生网络和教师网络在隐藏层的相似度差异；

3.中间层的回归损失（均方误差，mse）：计算学生网络和教师网络在中间层的均方误差

引言

边缘计算应用需要深度神经网络的压缩。在众多的网络压缩范式中，剪枝已经被证明是高效和实用的。网络剪枝的目标是从给定的网络中去除冗余参数，以使模型更轻量化，并潜在地加快推理速度。主流剪枝方法大致可分为两类：结构化剪枝和非结构化剪枝。

• 结构化剪枝：通过从物理上去除分组参数来改变神经网络的结构；
• 非结构化剪枝：对部分权值进行调零，而不修改网络结构。

在实践中非结构化剪枝能够直接地实现并且天然适用于各种网络，但它通常需要专门的人工智能加速器或软件来实现模型加速。而结构化剪枝不依赖于特定的人工智能加速器或软件来减少内存消耗和计算成本，应用更广泛。

挑战1：

深度神经网络建立在大量的基本模块之上，如卷积、标准化或激活，然而这些模块，无论参数化或未参数化，都是通过复杂的连接内在耦合的。因此，即使我们试图从CNN中只删除一个channel（如图1a），我们必须同时处理它对所有层的相互依赖关系。（这张图中，残差连接需要两个conv的参数来共享channel，所以修改conv2需要同时修改conv1，BN1，BN2）

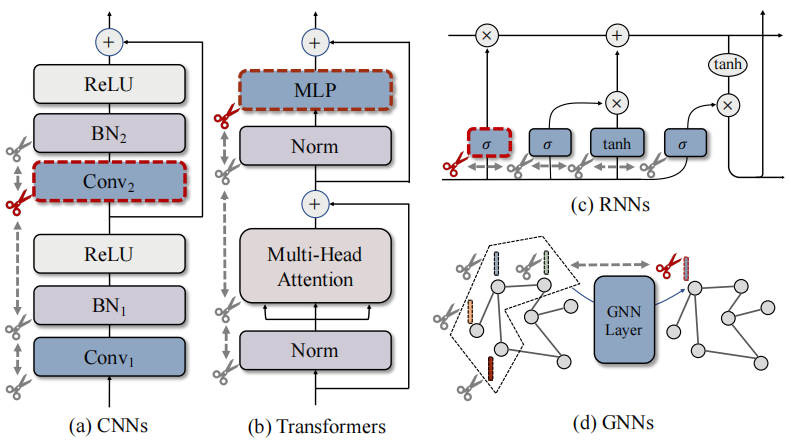
（图1：来自不同层的参数在跨网络架构中本质上是相互依赖的，这迫使多个层必须同时被修剪。本文引入了一个通用的方案，称为依赖图，以显式地解释这种依赖，并以全自动的方式对任意架构执行修剪。）

• 依赖性不仅出现在残差结构中，在现代模型中可能是无限复杂的。现有的结构化剪枝方案都依赖于个案分析，也就是针对于特定的网络。虽然效果好但费时费力且不能推广。
• 本文模型为了跟踪不同层之间的依赖关系，将依赖链分解并建模为一个递归过程，这自然可以归结为在图中寻找最大连通分量的问题，并且可以通过图遍历来实现O (N)复杂度。具体来说，对于网络中要修剪的层，可以将其作为根来触发相邻耦合层上的修剪，然后继续以被触发层为起点递归重复触发过程。通过这样做，可以全面收集所有耦合层以进行修剪。

挑战2：

在结构剪枝中，分组层同时被修剪，这期望同一组中所有被删除的参数都是不重要的。这样的话，由于和其他层之间的关联，在单层中的参数重要性就不能反映真实情况。在不同的层上估计的重要性很可能是非加性的，有时甚至是相互矛盾的，这使得很难选择真正不重要的组来进行修剪。

为了解决这个问题，本文利用DepGraph的依赖建模能力设计了一个“分组级别”的重要性标准，该准则学习组内的一致稀疏性，以便可以安全地删除那些归零的层，而不会造成太多的性能损失。通过依赖建模，在实验中表明了一个简单的L2范数准则可以达到与现代方法相当的性能。

总之，本文的贡献是针对任何结构修剪的通用修剪方案，称为依赖图（DepGraph），它允许自动参数分组，并有效地提高了各种网络架构（包括CNN、RNN、GNN和Vision Transformer）上结构修剪的可推广性。

相关工作

• 剪枝：剪枝算法的设计空间包括一系列方面，包括剪枝方案、参数选择、层稀疏性和训练技术。近年来，人们引入了许多稳健的标准，如基于幅度的标准和基于梯度的标准。另一种类型的方法通过稀疏训练来区分不重要的参数，稀疏训练将一些参数推到零以进行修剪。与那些静态标准相比，稀疏训练更可能找到不重要的参数，但由于需要网络训练，因此需要更多的计算资源。最近，还进行了一项综合性研究，以评估各种标准的效果，并提供一个公平的基准。

• 修剪分组参数：依赖性建模是任何结构修剪的关键和前提步骤，因为它涉及同时删除由于复杂的网络架构而在结构上彼此耦合的参数。剪枝分组参数的概念从结构剪枝的早期就已被研究。例如，当修剪两个连续卷积层时，修剪第一层内的卷积核会导致在后续层中去除与该滤波器相关的核。最近，已经提出了一些试点工作来解决层之间的复杂关系，并利用分组属性来提高结构修剪性能。

  不幸的是，现有的技术仍然依赖于经验规则或预定义的架构模式，这使得它们在所有结构剪枝应用程序中都不够通用。在本研究中，我们提出了一种解决这一挑战的通用方法，证明了解决参数依赖性有效地推广了广泛网络的结构剪枝，从而在多个任务上获得令人满意的性能。

本文方法

神经网络的依赖性

不失一般性，在全连接层开发本文方法。从由三个连续层组成的线性神经网络开始，如图2 (a)所示，分别由二维权重矩阵wl、wl+1和wl+2参数化。这种简单的神经网络可以通过去除神经元的结构修剪而变得轻量化。在这种情况下，很容易发现参数之间存在一些依赖关系，表示为wl⇔wl+1, 这迫使二者同时被修剪。具体而言，为了修剪连接wl和wl+1的第k个神经元，将移除wl [k, :]和wl+1[:, k]。

当我们希望通过剪枝某个神经元（高亮表示）实现加速时，与该神经元相连的多组参数需要被同时移除，这些参数就组成了结构化剪枝的最小单元，通常称为组（Group）。然而，在不同的网络架构中，参数的分组方式通常千差万别。图2（b）-（d）分别可视化了残差结构、拼接结构、以及降维度结构所致的参数分组情况，这些结构甚至可以互相嵌套，从而产生更加复杂的分组模式。

通过手动设计和模型特定的方案来处理层依赖性，以逐个案例的方式手动分析所有这些依赖关系是很难的，更不用说简单的依赖关系可以嵌套或组合成更任意复杂的模式。

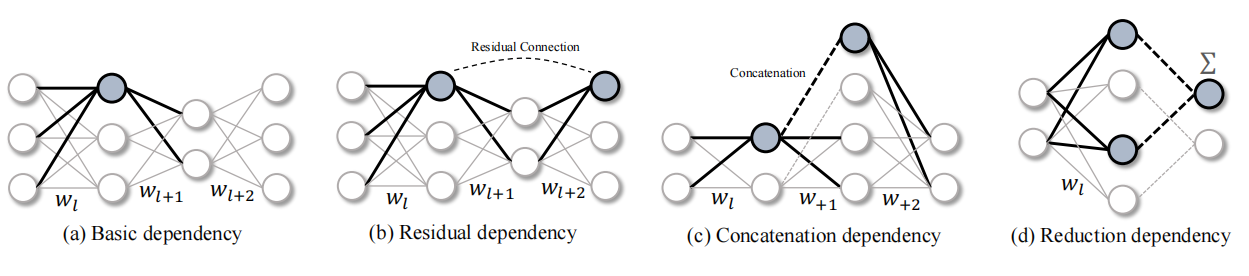
（图2：在不同的结构中具有相互依赖性的分组参数。必须同时修剪所有突出显示的参数。）

为了解决结构修剪中的依赖问题，在本文工作中引入了依赖关系图，它为依赖关系建模提供了一种通用的、全自动的机制。

依赖图

分组

为了实现结构化剪枝，首先需要根据层之间的相互依赖关系进行分组。形式上，目标是找到一个分组矩阵G∈R^L*L，其中L是一个待修剪网络的深度，Gij=1表示第i层和第j层之间存在依赖关系。令Diag(G)=1^1×L来保证自依赖。使用分组矩阵，很容易找到所有与第i层相互依赖的耦合层，即找到组：

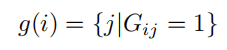
然而，由于现代深度网络可能由数千层复杂的连接组成，从神经网络中估计分组模式并不简单，他可能产生一个大而复杂的分组矩阵G。在这个矩阵中，Gij不仅由第i层和第j层决定，而且还受到它们之间的中间层的影响。这种非局部隐式关系在大多数情况下都不能用简单的规则来处理。为了克服这一挑战，作者没有直接估计分组矩阵G，而是提出了一种等效但易于估计的依赖建模方法，即依赖图，从中可以有效地推导出G。

依赖图

考虑一个分组g = {w1, w2, w3}，其中存在依赖关系w1⇔w2，w2⇔w3和1⇔w3。可以观察到冗余依赖（例如w1到w3可以通过w1w2，w2w3来推出传递依赖）。首先，我们以w1为起点，并检查它对其他层的依赖性，例如w1⇔w2。此时w2作为新的起点以递归扩展依赖，触发w2⇔w3，这个递归过程最终以一个传递关系结束，w1⇔w2⇔w3。在这种情况下，我们只需要两个依赖关系来描述组g中的关系。类似地，第3.2节中讨论的分组矩阵对于依赖关系建模也是冗余的，因此可以在保留相同信息的同时，压缩成更少的边和更紧凑的形式。

一种新的图D测量相邻层之间的局部相互依赖性，称为依赖图，可以作为分组矩阵G的有效约简。

依赖图只记录具有直接连接的相邻层之间的依赖关系。他具有和G一样的顶点，但是有尽可能少的边。形式上，D被构造为，对于所有的Gij = 1，在顶点i和j之间存在一条路径。因此，Gij可以通过检验D中顶点i和j之间的路径的存在来得到。

网络分解

在层级之间构建依赖图在实践中可能存在问题。一些基本层，如全连接层，可能有两种不同的修剪方案，如w[k, : ]和w[ : , k]，它们分别压缩输入和输出的维度（如前面图2所示，同样的全连接层，要考虑两种剪枝）。此外，网络还包含非参数化的操作，如跳跃连接，这也会影响层[40]之间的依赖性。

对于一个卷积层而言，我们可以对参数的不同维度进行独立的修剪，从而分别剪枝输入通道或者输出通道。然而，上述的依赖图D却无法对这一现象进行建模。为此，我们提出了一种更细粒度的模型描述符，将网络F（x；w）分解为更精细、更基本的组件，记为F = {f1，f2，…，fL}，其中每个组件f表示（1）一个参数层如卷积层 或者（2）一个非参数操作如残差连接。关注层的输入和输出之间的关系而不是在层之间建模。具体地说，将分量fi的输入和输出分别表示为𝑓𝑖−和𝑓𝑖+。对于任何网络，最终的分解都可以形式化为F = {𝑓1−，𝑓1+，…，𝑓L−，𝑓L+}。这种表示法更容易进行依赖关系建模，并允许对同一层使用不同的剪枝方案。

依赖建模

利用这种符号，我们将神经网络重新定义为方程2，其中可以识别出两种主要的依赖类型，即层间依赖和层内依赖，如下所示：

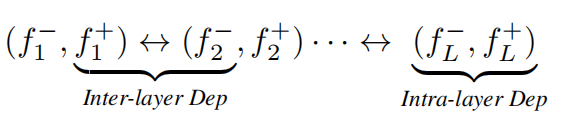
符号↔表示两个相邻层之间的连通性。对这两个依赖关系的检查产生了简单但通用的依赖关系建模规则：

• 层间依赖性：依赖性fi−⇔fj+持续出现在连接层中，其中𝑓𝑖−↔𝑓j+。由于一个层的输出和下一层的输入对应的是同一个中间特征（Feature），这就导致两者需要被同时剪枝。例如在通道剪枝中，“某一层的的输出通道剪枝”和“相邻后续层的输入通道剪枝”是等价的。

• 层内依赖性：在神经网络中，我们可以把各种层分为两类：第一类层的输入输出可以独立地进行剪枝，分别拥有不同的剪枝布局（pruning scheme），记作 𝑠𝑐ℎ(𝑓𝑖+) 或者 𝑠𝑐ℎ(𝑓𝑖−) 。例如对于全连接层的2D参数矩阵 𝑤 ，可以得到 𝑤[𝑘,:] 和 𝑤[:,𝑘] 两种不同的布局。这种情况下，输入 𝑓𝑖− 和输出 𝑓𝑖+ 在依赖图中是相互独立、非耦合的；而另一类层输入输出之间存在耦合，例如逐元素运算、Batch Normalization等。他们的参数（如果有）仅有一种剪枝布局，且同时影响输入输出的维度。如果 𝑓𝑖− 和 𝑓𝑖+ 共享相同的修剪方案，则存在依赖 𝑓𝑖− ⇔ 𝑓𝑖+ ，用𝑠𝑐ℎ(𝑓𝑖-) =𝑠𝑐ℎ(𝑓𝑖+) 表示。实际上，相比于复杂的参数耦合类型，深度网络中的层类型是非常有限的，我们可以预先定义不同层的剪枝布局来确定图中的依赖关系。

正式定义如下的依赖关系建模：

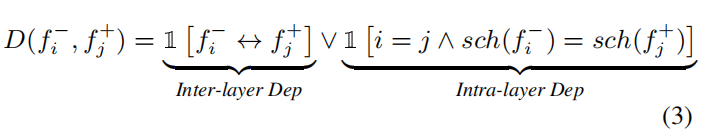
其中 ∨ 和 ∧ 分别表示逻辑”OR“和“AND”。第一项检查由网络连接引起的层间依赖关系，而第二项检查由层输入和输出之间的共享剪枝方案所引入的层内依赖关系。

我们在算法1和算法2中总结了依赖图构建和参数分组的过程，其中参数分组是一个递归的连通分量（Connected Component）搜索问题，可以通过简单深度(DFS)或者宽度(BFS)优先搜索实现。算法2简要描述了这一过程，即以某个节点i作为起始分组g，找到依赖图D中与之相连的新节点j，合并入当前组，直到不存在新的联通节点为止。此处省略了分组的去重处理。

将上述算法应用于一个具体的残差结构块，我们可以得到如下可视化结果。在具体剪枝时，以任意一个节点作为起始点，例如以 𝑓4+ 作为起点，递归地搜索能够访问到的所有其他节点，并将它们归入同一个组进行剪枝。值得注意的是，卷积网络由于输入输出使用了不同的剪枝布局（ 𝑠𝑐ℎ(𝑓4−)≠𝑠𝑐ℎ(𝑓4+) ），在依赖图中其输入输出节点间不存在层内依赖，但是由于skip连接 𝑓7 的存在，递归搜索过程中 𝑓4−和 𝑓4+ 会被分入同一组，即他们依旧需要被同时裁剪。其他层例如Batch Normalization的输入输出则存在简单的层内依赖。

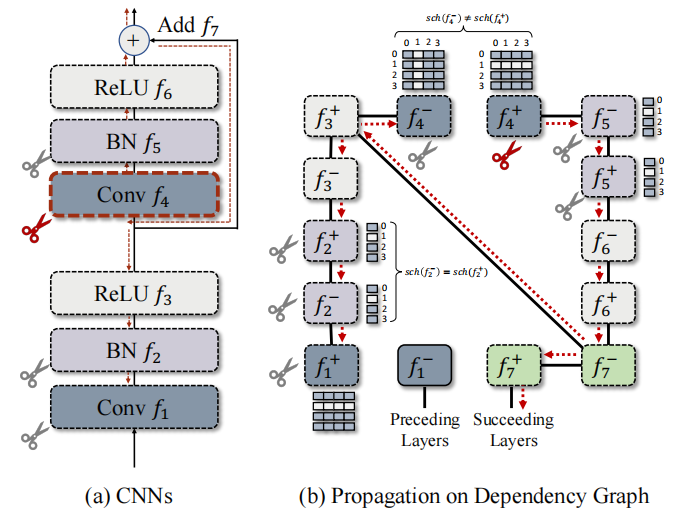
图3。层分组是通过在DepGraph上递归传递实现的（从f4+开始）

组级别剪枝

依赖图的一个重要作用是参数自动分组，从而实现任意架构的模型剪枝。实际上，依赖图的自动分组能力还可以帮助设计组级别剪枝（Group-level Pruning）。在结构化剪枝中，属于同一组的参数会被同时移除，这一情况下需要保证这些被移除参数是“一致冗余”的，如果这些参数中包含对网络预测至关重要的参数，那么移除这些参数难免会损伤性能。

一个重要问题是如何在涉及多个耦合层的情况下评估分组参数的重要性程度。在本节中，作者利用一个简单的norm-based标准来建立一个实用的组级剪枝方法。给定一个参数组g = {w1，w2，…，w|g|}，现有的标准如L2-norm重要性可以对每一个w产生独立的分数。估计组重要性的一种自然方法是计算一个聚合分数I(g)=每层分数的求和。但独立估计的各层重要性程度是非加性的，且由于分布和大小的散度而毫无意义。

为了使这个简单的聚合能够作用于重要性估计，我们提出了一种稀疏训练方法来在组级别上稀疏参数（如图4(c)），这些零化的组就可以安全地从网络中移除。

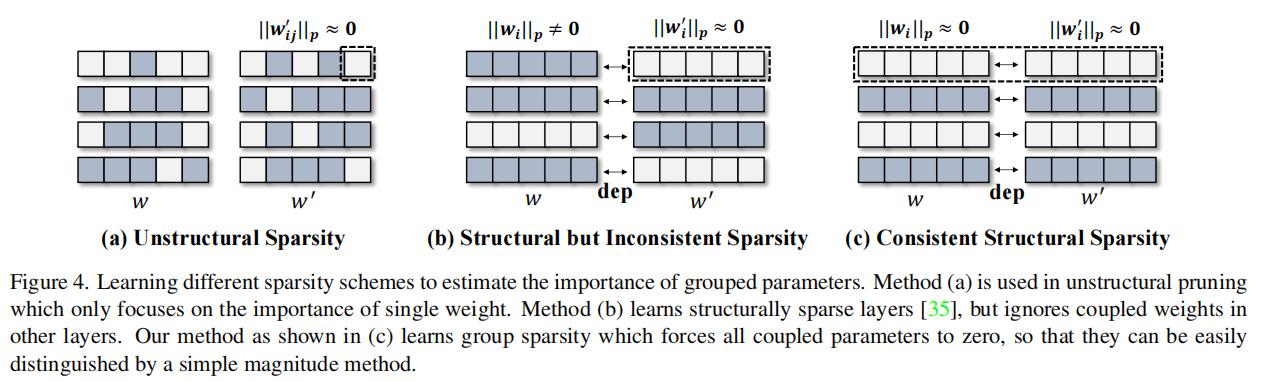
如图4 (c)所示，目标是学习所有分组层之间的一致稀疏性，同时将某些维度归零为零。作者将分组参数扁平化并合并为一个大的参数矩阵（也就是对于分组中的每一层，获取到特定通道的独立的参数组重要性后，展平，然后添加到分组重要性list，构成二维矩阵），其中检索所有属于第k个可调维数的参数，就像CNN块的第k个通道一样。现在，一致的稀疏性可以通过一个简单的加权收缩来促进（采用一个L2正则项，通过赋予参数组的不同正则权重 𝛾 来进行组稀疏化）

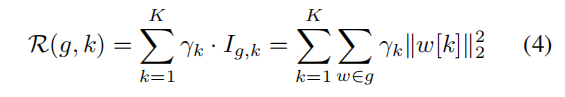
其中k用于可剪枝参数的切片（Slicing），用于定位当前参数内第k组参数子矩阵，上述稀疏算法会得到k组不同程度稀疏的耦合参数，我们选择整体L2 norm最小的耦合参数进行剪枝。我们使用一个可控的指数策略来确定γk如下：

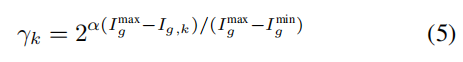
经过稀疏训练后，作者进一步使用了一个相对分数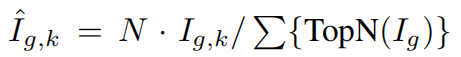来识别和删除不重要的参数。

实际上，依赖图还可以用于设计各种更强大的组剪枝方法，但由于稀疏训练、重要性评估等技术并非DepGraph的主要内容，这里也就不再赘述。

实验

设置

本文主要关注分类任务，在各种数据集上进行广泛的实验，如用于图像分类的CIFAR和ImageNet，用于图形分类的PPI，用于三维分类的ModelNet，用于文本分类的AGNews。使用模型如概要所述。为了进行ImageNet实验，使用了Torchvision 的现成模型作为原始模型。修剪后，所有模型都将按照与预训练阶段相似的协议进行微调，使用更小的学习率和更少的迭代。

性能

CIFAR是一个小型的图像数据集，被广泛用于验证剪枝算法的有效性。

我们利用DepGraph和一致性稀疏构建了一个非常简单的剪枝器，能够在这两种数据集上取得不错的性能。 当然，我们在Imagenet上并没有达到SOTA，因为我们的目标在于通用性而非特定架构上的性能。

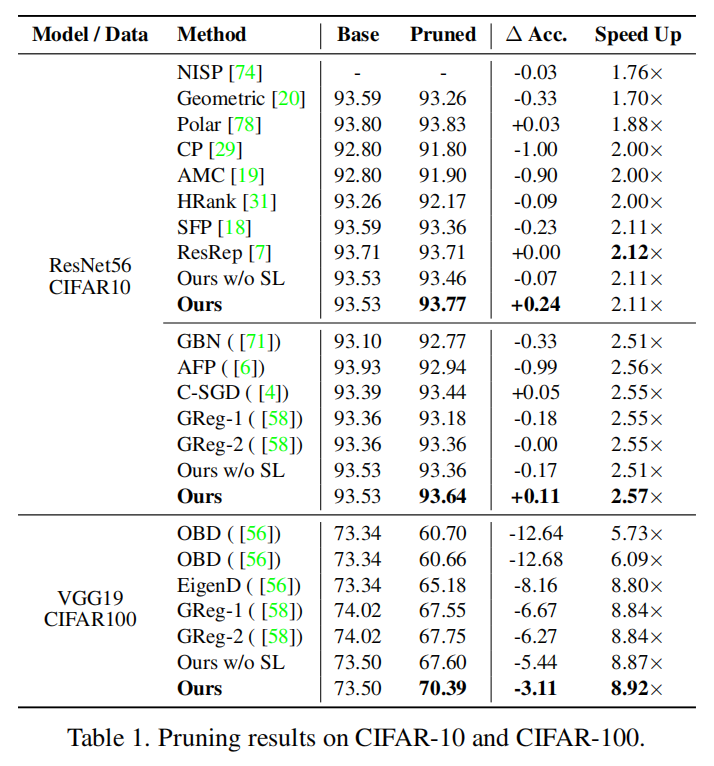
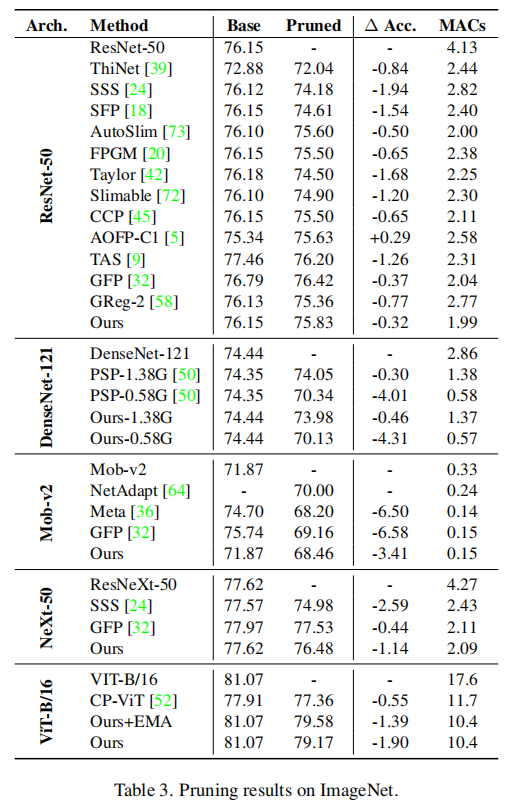
分析

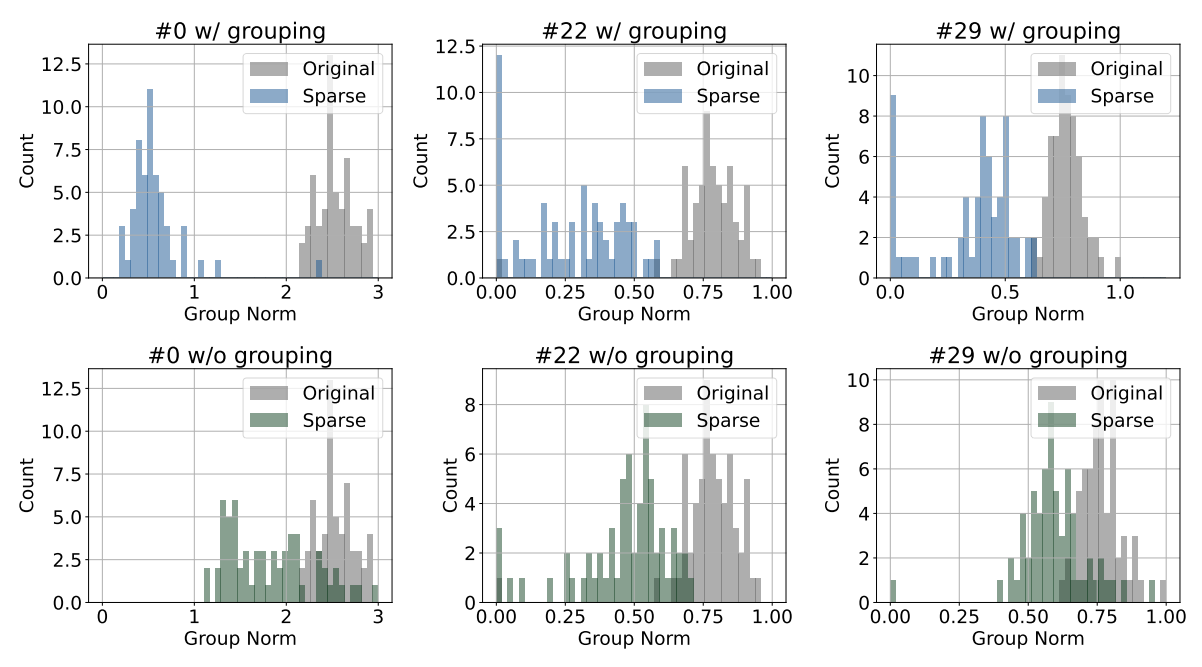
一致性稀疏

在分析实验中，首先我们首先评估了一致性稀疏和逐层独立稀疏的差异，结论符合3.3中的分析，即逐层算法无法实现依赖参数的一致稀疏。例如下图中绿色的直方图表示传统的逐层稀疏策略，相比于本文提出的一致性稀疏，其整体稀疏性表现欠佳。

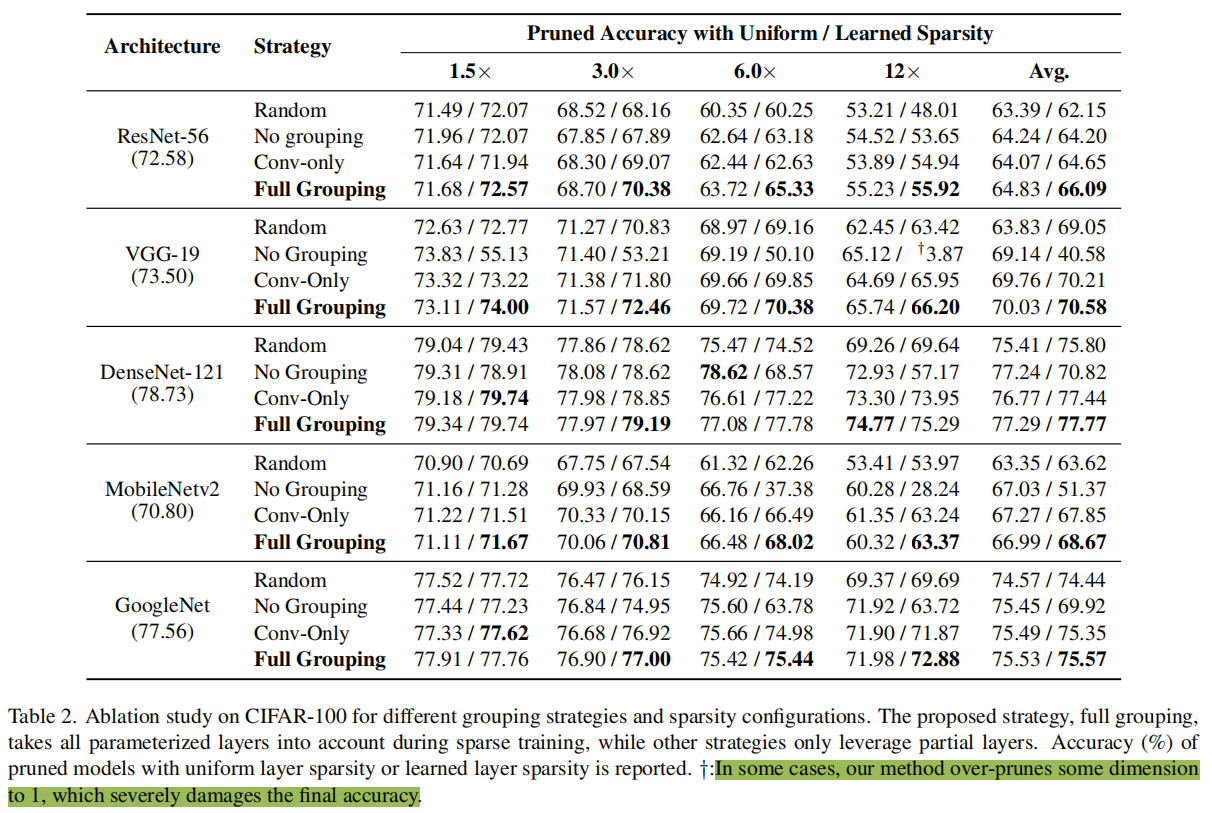
分组策略

我们同样对分组策略进行了评估，我们考虑了无分组（No Grouping）、卷积分组（Conv-only）和全分组（Full Grouping）三种策略：无分组对参数进行独立稀疏；卷积分组只考虑卷积层而忽略其他参数化的层；全分组将所有参数化的层进行一致性稀疏。实验表明全稀疏在得到更优的结果同时，剪枝的稳定性更高，不容易出现过度剪枝的情况（性能显著下降）。

另外剪枝的稀疏度如何分配也是一个重要问题，我们测试了算法在逐层相同稀疏度（Uniform Sparsity）和可学习稀疏度（Learned Sparsity）下的表现。可学习稀疏度根据稀疏后的参数L2 Norm进行全局排序，从而决定稀疏度。这一方法假设参数冗余并不是平均分布在所有层的，对不同层应用了不同的剪枝率，因此一般情况下可以取得更好的性能，这类方法通常也称为全局剪枝（Global Pruning）。但与此同时，可学习的稀疏度存在过度剪枝风险，即在某一层中移除过多的参数。下图中可以看到VGG网络出现了过度剪枝的问题，导致Learned Sparsity效果显著低于Uniform Sparsity。在实际应用中，还是需要根据具体网络、评估指标的特点选择合适的稀疏度分配策略。

可学习稀疏度

层的稀疏性也是剪枝的一个重要因素，它决定了剪枝神经网络的最终结构。表2提供了关于层稀疏性的一些结果。本研究主要关注两种稀疏性，即逐层相同稀疏性和可学习稀疏性。在相同稀疏性的情况下，由于假设了冗余参数通过网络均匀分布，所以对不同的层采用相同的剪枝比。然而，图5中之前的实验表明，不同的层并不是相同的。在大多数情况下，可学习的稀疏性优于均匀的稀疏性，尽管有时它可能会过度修剪某些层，导致精度下降。

DepGraph的通用性

表2中的结果也证明了我们的框架的通用性，它能够处理各种卷积神经网络。此外，我们强调我们的方法与DenseNet和GoogleNet兼容，它们包含密集的连接和并行结构。

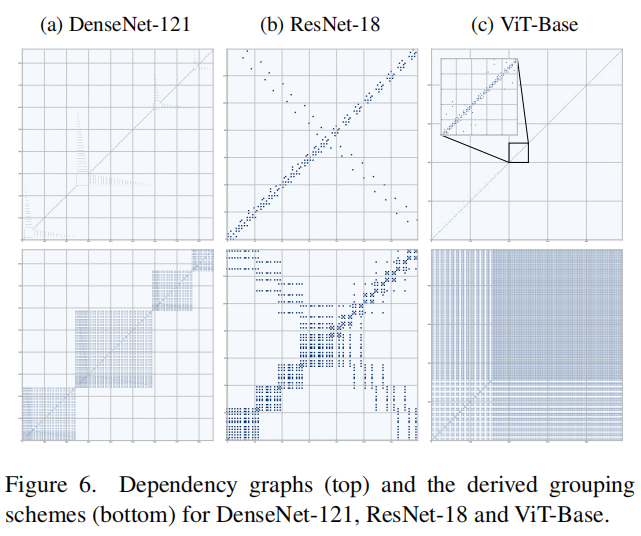
依赖图可视化

由于参数分组的复杂过程，修剪大型神经网络是一个相当大的挑战。然而，通过利用深度图，可以毫不费力地得到所有的耦合群。下图中我们可视化了DenseNet-121、ResNet-18、ViT-Base的依赖图和递归推导得到的分组矩阵，可以发现不同网络的参数依赖关系是复杂且各不相同的。

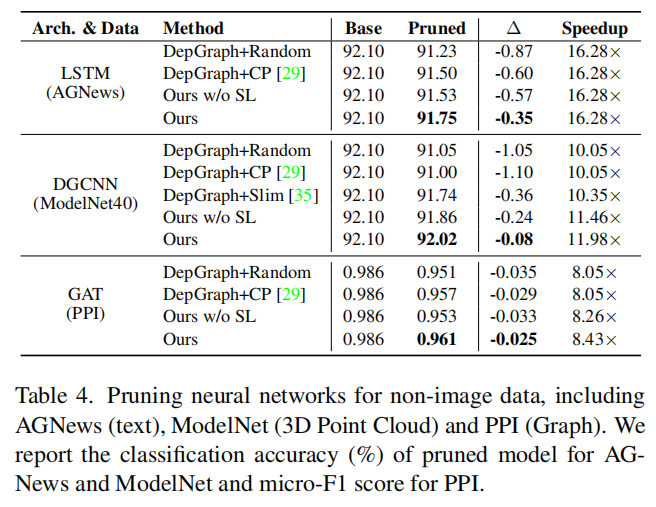
非图像模型结构化剪枝

深度模型不仅仅只有CNN和transformer，我们还对其他架构的深度模型进行了初步验证，包括用于文本分类的LSTM，用于3D点云分类的DGCNN以及用于图数据的GAT，我们的方法都取得了令人满意的结果。

总结

本文提出了一种面向任意架构的结构化剪枝技术DepGraph，极大简化了剪枝的流程。目前，我们的框架已经覆盖了Torchvision模型库中95%的模型，涵盖分类、分割、检测等任务。总体而言，本文工作是第一次尝试开发一种可应用于多种架构（CNNs, RNNs, GNNs, and Transformers）的通用算法。此外，当前大多数剪枝算法都是针对单层设计的，我们的工作为将来“组级别剪枝”的研究提供了一些有用的基础资源。

算法实现

权值剪枝器（Magnitude Pruner）

MagnitudePruner是一种利用权值大小定位冗余参数的经典算法，相关技术发表于“Pruning Filters for Efficient ConvNets”一文。作者讨论了一种神经网络中最基础的依赖关系（卷积和残差连接）

tp实现

类tp.importance.Importance要求我们实现一个非常简单的接口__call__，其中输入参数是一个group，它包含了多个相互耦合的层。该函数的输出则是一个一维的重要性得分向量，其含义是每个通道的重要性，因此他的维度和通道数通常是相同的。由于输入的Group通常会包含多个可剪枝层，因此我们首先对这些层进行独立的重要性计算，然后通过求平均值得到最终结果。

import torch
import torch.nn as nn
import torch_pruning as tp

class MyMagnitudeImportance(tp.importance.Importance):
    def __call__(self, group, **kwargs):
        # 1. 首先定义一个列表用于存储分组内==每一层==的重要性
        group_imp = [] 
        # 2. 迭代分组内的各个层，对Conv层计算重要性
        for dep, idxs in group: # idxs是一个包含所有可剪枝索引的列表，用于处理DenseNet中的局部耦合的情况
            layer = dep.target.module # 获取 nn.Module
            prune_fn = dep.handler    # 获取 剪枝函数
            # 3. 这里我们简化问题，仅计算卷积输出通道的重要性
            if isinstance(layer, nn.Conv2d) and prune_fn == tp.prune_conv_out_channels:
                w = layer.weight.data[idxs].flatten(1) # 用索引列表获取耦合通道对应的参数，并展开成2维
                local_norm = w.abs().sum(1) # 计算==每个通道参数子矩阵的 L1 Norm==
                group_imp.append(local_norm) # 将其保存在列表中

        if len(group_imp)==0: return None # 跳过不包含卷积层的分组
        # 4. 按通道计算平均重要性
        group_imp = torch.stack(group_imp, dim=0).mean(dim=0) 
        return group_imp 

对于每个Group，我们计算了其中卷积层输出通道的重要性，然后求平均值得到最终的评估结果。基于上述代码，一个MagnitudePruner实际上已经完成了，但是参数修剪由谁来执行呢？Torch-Pruning库定义了一个元剪枝器tp.pruner.MetaPruner，能够帮助我们完成除了重要性评估之外的所有工作。因此，我们现在可以开始执行剪枝了。为了增加难度，这里我们对一个DenseNet模型进行剪枝：

import torch
from torchvision.models import densenet121
import torch_pruning as tp

model = densenet121(pretrained=True)
example_inputs = torch.randn(1, 3, 224, 224)

# 1. 使用我们上述定义的重要性评估
imp = MyMagnitudeImportance()

# 2. 忽略无需剪枝的层，例如最后的分类层
ignored_layers = []
for m in model.modules():
    if isinstance(m, torch.nn.Linear) and m.out_features == 1000:
        ignored_layers.append(m) # DO NOT prune the final classifier!

# 3. 初始化剪枝器
iterative_steps = 5 # 迭代式剪枝，重复5次Pruning-Finetuning的循环完成剪枝。
pruner = tp.pruner.MetaPruner(
    model,
    example_inputs, # 用于分析依赖的伪输入
    importance=imp, # 重要性评估指标
    iterative_steps=iterative_steps, # 迭代剪枝，设为1则一次性完成剪枝
    ch_sparsity=0.5, # 目标稀疏性，这里我们移除50%的通道 ResNet18 = {64, 128, 256, 512} => ResNet18_Half = {32, 64, 128, 256}
    ignored_layers=ignored_layers, # 忽略掉最后的分类层
)

# 4. Pruning-Finetuning的循环
base_macs, base_nparams = tp.utils.count_ops_and_params(model, example_inputs)
for i in range(iterative_steps):
    pruner.step() # 执行裁剪，本例子中我们每次会裁剪10%，共执行5次，最终稀疏度为50%
    macs, nparams = tp.utils.count_ops_and_params(model, example_inputs)
    print("  Iter %d/%d, Params: %.2f M => %.2f M" % (i+1, iterative_steps, base_nparams / 1e6, nparams / 1e6))
    print("  Iter %d/%d, MACs: %.2f G => %.2f G"% (i+1, iterative_steps, base_macs / 1e9, macs / 1e9))
    # finetune your model here
    # finetune(model)
    # ...
print(model)

Slimming剪枝器

在上文中，我们介绍了如何快速实现一个简单的权值剪枝算法，它直接作用于模型的参数上，选取那些相对较小的参数进行裁剪。然而，实际上一个模型中的各个参数权值大小可能非常接近，因此我们难以直接根据参数大小来判断其重要性。针对这一问题，于ICCV2017会议上发表的slimming算法提出了一种经典的解决方案：利用Batch Normalization的scale参数完成重要性评估。

…………

LLM剪枝

任务

LLM压缩与传统网络压缩区别：

1. 模型规模：第一个主要差异来自LLM的巨大参数量，这导致许多侧重训练（Training-heavy）的压缩方案，例如知识蒸馏[1]变得较为困难.

2. 海量训练语料：许多LLMs经历了1万亿甚至更大规模的tokens上的训练[3]，这导致许多依赖于原始数据或收集替代数据的方案变得尤其昂贵。

3. 任务无关的模型压缩：现有的压缩算法通常针对单一、特定的任务进行压缩，而LLMs是很优秀的多任务处理器，在压缩过程中我们不希望折损LLM的通用性和多功能性。

我们需要一种能够避免大规模重新训练、且能保持模型原有能力的压缩方法。现有的较为可行的两种方案是【模型量化】和【网络剪枝】。其中模型量化侧重于降低推理阶段的存储开销以及提升计算速度，而网络剪枝则移除部分参数实现压缩，两种方案可以相互结合达到最优性能。

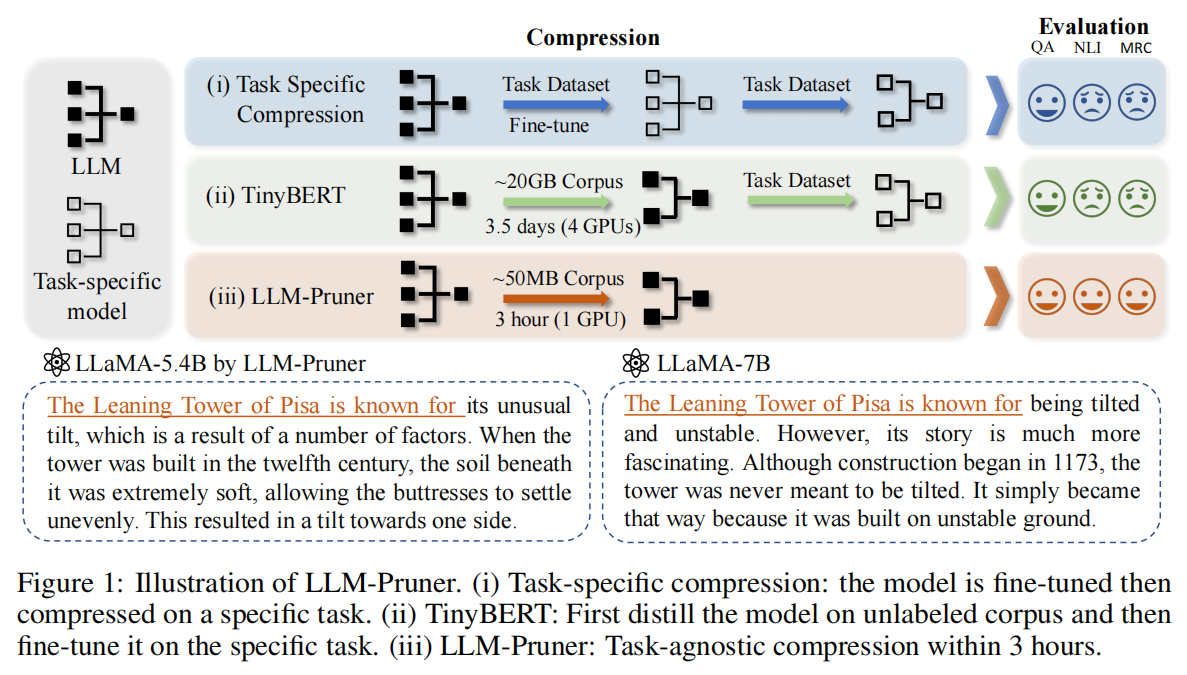
挑战

1.训练语料库规模巨大：以往的压缩方法严重依赖于训练语料库。LLM已经将语料库规模升级到1万亿token。巨大的存储需求和漫长的传输时间使数据集难以获取。

2.修建后的LLM的后训练时间巨大：现有的方法需要大量的时间来后训练生成的小模型。例如，在TinyBERT中的一般蒸馏大约需要14 GPU天。即使是后训练特定任务的BERT压缩模型也需要大约33小时。随着llm的模型和语料库的大小迅速增加，这一步骤必然会消耗更长的时间。

方法

遵循常规的剪枝流程，LLM-Pruner包含三个步骤：发现阶段，估计阶段，恢复阶段。

(1) 发现阶段：这一步聚焦于识别LLM内部相互依赖的结构，这些相互依赖的结构需要被同时移除已确保剪枝后结构的正确性。

(2) 估计阶段：一旦耦合结构被分组，第二步就包含估计每个组对模型总体性能的贡献，并决定要剪枝的组。

(3) 恢复阶段：这一步涉及到快速的后训练，用于缓解由于结构删除而可能引起的性能降级。

依赖分组

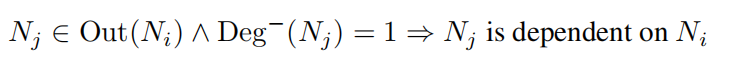
Ni指向Nj，且Nj入度为1。则Nj依赖于Ni。

Nj唯一依赖于Ni，则Ni与Nj在同一组

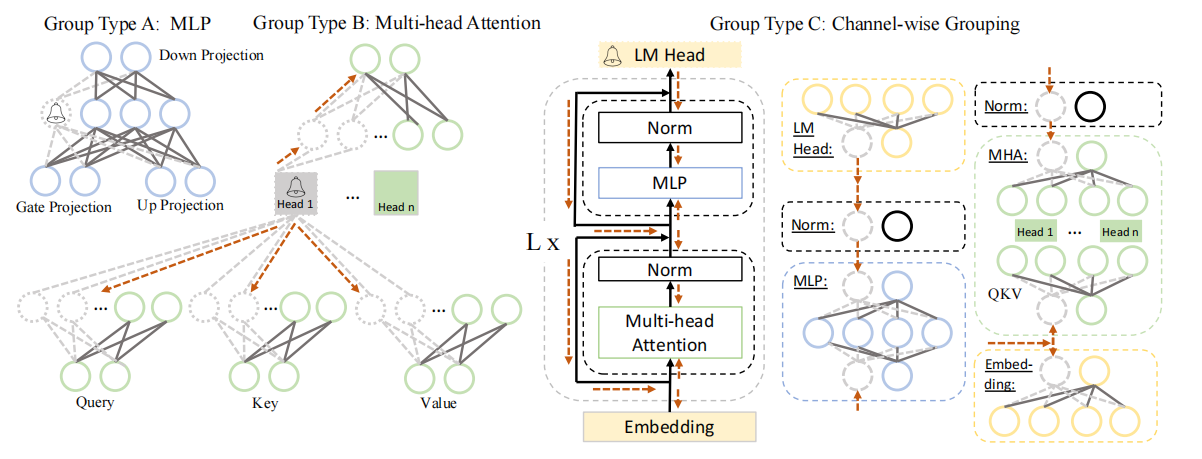
图2: LLaMA中耦合结构的示例。我们简化了每层的神经元以清晰地展示依赖组。剪枝的起始神经元被铃图案所标记，这一操作会导致具有依赖性的权重被剪枝（虚线），并继续传播到耦合神经元（虚线圆圈）

参考

CVPR 2023 | DepGraph 通用结构化剪枝：https://zhuanlan.zhihu.com/p/619146631

模型加速｜CNN与ViT模型都适用的结构化剪枝方法（一）：https://developer.aliyun.com/article/1231617

【深度学习之模型优化】模型剪枝、模型量化、知识蒸馏概述：https://blog.csdn.net/qq_51831335/article/details/126660743

Torch-Pruning | 轻松实现结构化剪枝算法： https://zhuanlan.zhihu.com/p/619482727

YOLOv8模型剪枝实战： https://www.bilibili.com/video/BV1iA4m1F7zf/?vd_source=bf952648bf410c0b9b23bf213e3d24ba

NeurIPS 2023 | LLM-Pruner: 大语言模型的结构化剪枝： https://zhuanlan.zhihu.com/p/630902012